Canadian Journal of Learning and Technology

Volume 33(2) Spring / printemps 2007

Using video in teacher education *

Jo Towers

Author

Jo Towers is an Associate Professor in the Faculty of Education at the University of Calgary. Her research interests include the teaching and learning of mathematics, the phenomenon of mathematical understanding, teacher education, and qualitative research involving video. Correspondence regarding this article can be sent to: towers@ucalgary.ca

Abstract: This paper draws on a research study of elementary- and secondary-route preservice teachers in a two-year, after-degree teacher preparation programme. The paper includes excerpts of classroom data, taken from the author’s own university classroom, demonstrating preservice teachers’ responses to carefully selected video extracts of children learning mathematics in a high-school class also taught by the author. The paper includes commentary on some of the advantages and limitations of video as a teaching tool, develops an argument for the increased use, in both preservice teacher education and inservice teacher professional development, of videotaped episodes that focus on the learners rather than on the classroom teacher, and explores the value of having the teacher whose classroom is featured on the videos present for the discussion of the episodes. The paper explores the potential offered by video material to foster the belief that teaching is a learning activity by (i) refocusing attention on the learner rather than the teacher in the analysis of classroom practices, (ii) raising awareness of the importance of reflective practice, and (iii) providing a prompt for the imaginative rehearsal of action.

Résumé : Le présent article se fonde sur une étude technique portant sur des stagiaires des niveaux primaire et secondaire dans un programme de préparation à l’enseignement de deux ans après l’obtention du diplôme. L’article comprend des extraits de données en salle de classe qui proviennent de la salle de classe de l’université de l’auteur même, illustrant les réponses des stagiaires à des extraits vidéo choisis avec soins, extraits portant su des enfants apprenant les mathématiques dans une classe du secondaire dont l’enseignant est l’auteur. L’article comporte des commentaires sur certains des avantages et limites du vidéo comme outil d’enseignement, il présente un argument pour l’augmentation accrue, à la fois pour l’éducation du stagiaire et le perfectionnement professionnel de l’enseignant qualifié, des épisodes sur cassette vidéo qui mettent l’accent sur les apprenants plutôt que sur les enseignants en salle de classe et examine s’il est intéressant que soit présent au moment de la discussion sur les épisodes l’enseignant dont la salle de classe figure sur le vidéo. L’article analyse le potentiel du matériel vidéo appuyant la croyance selon laquelle l’enseignement est une activité d’apprentissage en (i) mettant l’accent sur l’apprenant plutôt que sur l’enseignant dans l’analyse des pratiques d’une salle de classe, (ii) en effectuant une sensibilisation relativement à l’importance de la pratique réflexive et (iii) en guidant la répétition novatrice de la mesure.

Introduction

Though numerous educational research studies testify to the use of video-recording as a major means of classroom data collection (see, e.g., Pirie & Kieren, 1994; Wood, Cobb, & Yackel, 1991), and there is a significant body of literature dealing specifically with the ways in which video can be employed as a data collection and analysis tool (see, e.g., Artzt & Armour-Thomas, 1992; Bottorff, 1994; Calderhead, 1981; Goldman-Segall, 1993; Marland, 1984; Pirie, 1996), it has been claimed that less attention has been paid to the use of videotaped episodes of classroom practice in the education and professional development of future and practising teachers (Masingila & Doerr, 2002). Some important examples exist, though, such as the work of Lampert and Ball (1990; 1998), Masingila and Doerr (2002), and Doerr and Thompson (2004). Selinger (1994) has also found that the use of video can “enhance student understanding of teaching” (p. 248), however as Ball (1995) notes, we know little about what people attend to and learn when watching videotape. Ball suggests, therefore, that what can be learned from videotape is worth investigating, and asks how the experience of viewing should be structured to generate learning.

Drawing explicitly on data collected in a study of elementary and secondary preservice teachers in a two-year after-degree teacher preparation programme, and also drawing more generally on my broader experience of using videotaped examples in preservice and inservice mathematics teacher education, this paper describes specific ways in which preservice teachers’ understanding of teaching may be enhanced through the use of videotaped examples, and explores the potential offered by video material to foster the belief that teaching is a learning activity by (i) refocusing attention on the learner rather than the teacher in the analysis of classroom practices, (ii) raising awareness of the importance of reflective practice, and (iii) providing a prompt for the imaginative rehearsal of action (Dewey, 1908/1932).

Theoretical Framework—A Phronetic Approach to Teaching and Learning

The broad theoretical perspective framing this research is centred on Aristotle’s conception of phronesis (Dunne, 1997, 2005), though I have also invoked elements of improvisational theory, drawn from the domains of jazz and theatre, to help characterise and account for particular collective classroom processes that have led to the growth of these students’ understandings of both the discipline of mathematics and mathematics-for-teaching (see, e.g., Towers & Martin, 2007). As Coulter and Wiens (2002) note, phronesis does not easily translate into English, but a common translation, and one adopted by the teacher education programme in which the students featured in this writing have participated, is practical wisdom. Phronesis is a particular kind of knowledge—one oriented to action, and specifically ethical action, action oriented to the good (Coulter & Wiens, 2002; Lund, Panayotidis, Smits, & Towers, 2006; Ricoeur, 1992; Wall, 2003). “This is knowledge not as a possession ... but as invested in action” (Dunne & Pendlebury, 2002, p. 198), and it is knowledge with an irreducible core of judgement. Phronesis hence requires an interaction between the general and the particular. It requires consideration, judgment, and choice (Flyvbjerg, 2001). This kind of knowledge contrasts sharply with a technical perspective on teaching, which

Seeks to extract from [practice] a rational core that can be made transparent and replicable. Typically, this entails disembedding the knowledge implicit in the skilful performance of the characteristic tasks of the practice from the immediacy and idiosyncrasy of the particular situations in which it is deployed, and from the background of experience and character in the practitioners in whom it resides. Through this disembedding it is supposed that what is essential in the knowledge and skill can be abstracted for encapsulation in explicit, generalisable formulae, procedures, or rules—which can in turn be applied to the various situations and circumstances that arise in the practice, so as to meet the problems they present. (Dunne, 2005, p. 375)

A phronetic approach to teaching calls forth from practitioners a set of capacities and practices that differ strongly from those valued within such a technical rationalist frame (Dunne & Pendlebury, 2002). These alternative practices include such capacities as an ability to differentiate teaching for diverse learners, dispositions such as attunement to the nuances of listening to learners, and classroom practices that foster investigation and problem-solving and that balance teacher-telling with authentic student engagement. Hence, rather than orienting beginning teachers to abstracting ‘rules’ of practice, using classroom video in the particular ways described in this article is a pedagogical strategy that is intended to help them develop practical wisdom—the knowledge, capacities and dispositions that are at the heart of reflective, inquiry-based practice that is focused on learners. The research presented here examines this pedagogical strategy.

Video in Teacher Education

In an informal publication directed to teachers, Jaworski (1989) promotes the use of videotape for professional development. Her publication proposes ways in which teachers can initiate and sustain discussion about video recordings taken from their own classrooms, or professionally produced recordings. Whilst I do not claim that video experiences are a substitute for teaching practice for preservice teachers, or a substitute for experience in real-life classroom situations for practising teachers, I do claim that there are some advantages to the use of videotaped episodes over other forms of representation of classroom activities, such as a text-based case study, for example, although I use, and see great value in, text-based case materials, too.

Pimm (1993) describes two common responses from adults (both teachers and teacher educators) as a result of being shown a piece of classroom videotape, which he has labelled televisual and intimidated. A televisual response is one that is based on the expectations that people have when a TV monitor is introduced into the room. Pimm suggests that on these occasions students tend to become passive—they have been conditioned by their usual experiences of television viewing to expect to be entertained, not stimulated intellectually. Pimm suggests that this response, whilst understandable and explicable, detracts from the value of using video. In contrast, I have found that offering preservice teachers video excerpts that feature my own high-school teaching promotes viewing that is far from passive. The preservice teachers recognise that they are being offered the relatively unusual opportunity of investigating an episode of teaching practice with the teacher who is featured on the video, and they respond enthusiastically and with interest. My students are aware of the fact that when the video is over they will have the opportunity to press me for more information than the video itself could provide. I therefore suggest that the impact of a televisual response can be reduced when the teacher whose classroom is featured on the video is present for the ensuing discussions and/or when the teacher educator has first-hand knowledge of the classroom depicted through his or her own participation as teacher or researcher in that classroom.

As Pimm (1993) also notes, beginning teachers are often intimidated by carefully selected extracts featuring experienced teachers and apparently highly motivated and responsive pupils. Pimm reports that this intimidation leads to defensiveness and that beginning (and more experienced) teachers often respond by criticising the teaching. In deliberately positioning my teaching as a space for critique I am encouraging my students to develop a critical voice, a perspective Britzman (1991) assures us does not destroy or devalue the struggle of others (in this case the on-screen teacher) but rearticulates the tensions between and within words and practices. Through such a rearticulation of the messy interplay between theory and practice I seek to lay open to scrutiny the complexity of the learning-teaching relationship, to legitimise pedagogical uncertainty, and to encourage beginning teachers to take up the deep difficulty of teaching, not as something to fear but as a lifelong learning endeavour. Some teacher educators (see, e.g., Smits, 1997), myself included, are concerned about the tendency, reinforced in some teacher education programmes by an emphasis on methods of teaching, for beginning teachers to view practice as a kind of application of theory. Theory and practice are often placed in opposition to one another, with practice commonly expressed as presenting reality and theory as re-presenting it (Gauthier, 1992). Engaging with me in theorising about, and through, my own practice is one way by which I hope to loosen preservice teachers’ convictions about the relative merits of theory and practice and broaden their perspectives about the complex role that theoretical discourses play in teachers’ lives.

AsBall (1995) notes, however, the challenge is one of developing in beginning teachers a stance that is less simply evaluative of the teaching they see and more analytic of practice. I acknowledge that there is value in also offering preservice (and practising) teachers opportunities to experience, through videotape or some other means, practice that is ‘exemplary’, for, as Ball (1990) and others (see e.g., Howey & Zimpher, 1999; Lampert & Ball, 1999) note, unless preservice teachers have experience of an alternative model of teaching to the traditional one that many of those of us who enter the teaching profession have experienced in our own schooling, then they cannot hope to be able to enact a different conception of what it means to teach when they are faced with the prospect of beginning to teach in their own classrooms. However, I do not believe that preservice (or practising) teachers necessarily need to experience how such an alternative conception can be enacted while they are in a school setting. Both the context of teacher education itself (e.g., Phelan, 2005) and an immersion in the “materials of practice” (Ball & Cohen, 1999) (such as the strategic documentation of practice represented by the kinds of videotape and supporting materials I offer to preservice teachers) can offer alternative conceptions of teaching that are rich and complex.

In addition to Pimm’s (1993) televisual and intimidated responses to viewing videotapes, Busher and Clark (cited in Prosser, 2000, p. 129) have proposed a third response—the rush to judgement of the teacher portrayed on the tape. This response is also one that seems to have been minimised by my use of videotapes in which I feature as the teacher. This is perhaps understandable, as student teachers could be expected to be somewhat reluctant to critique their university professor’s teaching—an idea I take up more fully later. Nevertheless, the instinct to tread carefully that surfaces as student teachers choose ways to articulate their critiques sensitively to me is an important skill to develop as they move into school settings and need to be able to both accept and interpret others’ (including administrators’) critiques of their own teaching and as they themselves gradually move into the role of mentor to newer teachers and take on the responsibility of offering critiques to others.

While there is a broad and growing body of literature concerned with documenting teaching and learning practices (e.g., Burnard et al., 2006; Giudici, Rinaldi, & Krechevsky, 2001; Harvard Project Zero, 2003; Niguidula, 2005; Smits, Wang, Towers, Crichton, Field, & Tarr, 2005; Szente, Massey, & Hoot, 2005), the capacity of videotape to allow for viewing and re-viewing of the same classroom episode multiple times, and to preserve a rich complement of contextual features of the classroom setting, are advantages fore-grounded by researchers interested in making teaching and learning practices more visible both for beginning teachers (Lampert & Ball, 1998) and researchers (Pirie, 1996). As Lampert and Ball (1998) note,

Teaching is uncertain and complex work, teachers are faced with having to construct knowledge as they work. ... [Hence] learning to teach entails learning how to construct and use knowledge in practice. ... Preservice teacher education, therefore, must seek to prepare teachers to reason wisely, to develop responses and courses of action in response to particulars, to extend and improvise beyond that which they have acquired or done before. ... What ... teacher education students need to develop is an increased capacity for judging what and when action is appropriate in a given time and place. (pp. 69–70)

Students therefore need opportunities for learning such nuanced practice, and repeated viewings of classroom video and the associated materials of practice (e.g., student work and teacher planning notes and reflections relating to the videotaped session, etc.) can provide such opportunities (Lampert & Ball, 1998, p. 77). Opportunities for repeated viewing of the video excerpts is particularly valuable in allowing for multiple interpretations and, indeed, re-interpretations, of actions or verbalisations witnessed on screen, as Pirie (1996) has previously noted and as has been evidenced in my own writings wherein repeated viewings of an episode of classroom action captured on videotape have revealed hidden student competencies and highlighted for me troubling aspects of my teaching practice (Towers, 1996a).

Methods and Methodological Issues

The episodes I describe here are taken from data collected in my university classroom during a study in which I followed a cohort of elementary and secondary students through an inquiry-based mathematics education course (three hours per week for 13 weeks) with me in their final semester of a two-year after-degree teacher preparation programme, and then traced their development as teachers of mathematics through their first year of full-time teaching, seeking to understand more about what, and how, they learned about mathematics teaching during their preservice education and about the ways in which they enacted their learning when in practice. Data sources include videotapes of all of my university teaching sessions with this group, my planning notes and my own journal entries, videotaped interviews with the preservice teachers during the final semester of their teacher education programme and during their first year of teaching, videotapes of the school classrooms in which these students completed their first year of teaching, and photocopies of the children’s mathematics work during those videotaped lessons.

I personally conducted the majority of data collection for this study. This included all video-recording in my own university classroom, a strategy that meant that I was not often able to change the direction or focus of the camera for this portion of the research. Despite this, I was able to shift the focus at key moments, as the action shifted from whole-class to small-group work and vice versa. I employed a similar strategy in videotaping in my high-school classroom, too, and hence the video-recordings in both settings have a particular flavour. For the most part, they focus on pairs or small groups of students, and I, as the teacher in both settings, appear only infrequently, usually at moments when I am called over by a student or when I drop in on a group to observe their progress. The microphone used is a high quality one, and picks up my voice when I speak to the whole class, even if I am not always within view of the camera at those moments. As Goldman-Segall (1998) has noted, who is pointing the camera, and at what, are significant methodological issues in video-based research. As my analysis of preservice teacher learning described in the following section of this paper shows, the particular point of viewing of my video records is significant and contributes to the tendency of the preservice teachers to focus closely on student learning rather than teacher performance. Doubtless, my own interpretations of what is significant to focus upon have been similarly coloured in my viewing of the action captured on camera in my university classroom and reported here.

Data analysis proceeded through an iterative process of viewing and re-viewing the video data and supporting evidence (such as field notes and copies of students’ work on classroom mathematics tasks), following the approach described by Powell, Francisco, and Maher (2003), itself a method that is influenced by the work of Pirie (1996, 1998, 2001) and Martin (1999). Initially, videotapes of the teacher education classroom events were viewed in their entirety to get a sense of their content and context, without imposing a specific analytical lens. In the second stage the video data were described through writing brief, time-coded descriptions of each video’s content. The aim was both to map out the video data for further analysis and to become more familiar with its content. In stage three the data (videotapes and coded notes) were reviewed to identify “critical events” (Maher, 2002). Stage four involved analysing and coding these identified critical events to create rich and detailed theoretical descriptions, linked to extracts of video data, of critical events in the process of learning to teach of a number of student teachers, over various time periods. The fifth stage of analysis involved examining closely these analysed and coded critical events to identify and construct a storyline to “discern an emerging and evolving narrative about the data” (Powell, Francisco, & Maher, 2003, p. 430). In the final stage of data analysis the storylines established for each research participant in stage five were reassembled to produce cross-case written narratives that speak to general themes in the data and address other aspects of the nature of learning to teach through inquiry. One such cross-case theme is addressed in this article—the role that engaging with classroom video extracts plays in preservice teachers’ learning . Works that speak to the overall research aims of the study have begun to be presented ( Lund, Panayotidis, Smits, & Towers, 2007; Towers & Martin, 2007) or are now in process (Towers, 2007a, 2007b).

In drawing on documented incidents from my own teaching practice this article augments the body of first-person writing about teaching, a body of research that Ball (2000) claims provides an important contribution to knowledge about practice. Ball suggests that such research can “access, uncover, and probe elements of the situation or experience invisible to the outsider” (p. 388), though she is careful to point out that not all questions or problems of practice are best addressed by an insider perspective. A key issue in this regard is whether or not what the researcher is addressing is uniquely accessible from the inside. I believe that I am uniquely placed to investigate the issue of the use of classroom videotape in structuring preservice teacher learning in this particular context, as I primarily use excerpts of classroom videotape taken from my own high-school teaching during periods of teacher-research activity as examples in my teacher education classroom. This renders my position one of being doubly an insider in terms of the research I describe here—reporting on self-study of my university teacher education practices in which I use videotapes featuring me as a high-school teacher. This multi-faceted role, while admittedly being somewhat unusual as a methodological approach to the study of teaching, retains many of the advantages of traditional self-study research. As Lampert and Ball (1998) note, it is a means of “seeking to learn in and from practice in ways that [are] both deliberate and reflective” (p. 23). By offering examples of my own high-school and university teaching as they are intertwined in this account, my teaching practice becomes a “text to be interpreted” (Lampert & Ball, 1998, p. 40) both by preservice teachers and by teacher educators.

Examples and Analysis of Video Use in Teacher Education

The Role of Video in Refocusing Attention on Learning

It is claimed that case teaching (of which the use of video extracts might be considered a part)draws students into the situations, problems, and roles portrayed, and that engaging with cases can therefore, in one sense, become like role-playing (Sykes & Bird, 1992). Placing students in a hypothetical role-playing situation creates a ‘safe’ environment for practice, but continues to privilege the role of the teacher over the perspectives of the students. In my use of video episodes I de-emphasise this role-playing attitude by orienting the preservice teachers to a focus on the students who are the focus of the videotapes. Though there is an eventual and inevitable progression to a consideration of the role of the teacher (see next section) it is not immediate, and it is not my main aim. Instead, beginning teachers are challenged to turn their attention outwards instead of inwards. I use the word challenge here in recognition of the fact that research has shown that, for a variety of reasons, beginning teachers tend to privilege their own perspective (as teacher) over the perspectives of the students they are to teach (Ball, 1988; Darling-Hammond, Hammerness, Grossman, Rust, & Shulman, 2005; Huinker & Freckmann, 2004; Merseth, 1993; Wilson, 1990). As Darling-Hammond et al. (2005) note, “research on new teachers indicates that they do not often begin with a focus upon student learning and are instead concerned with their own actions in the classroom” (p. 400).

The videotapes I choose focus closely on a pair of students in each of the classes I videotaped². The picture never pans out to reveal the rest of the class, or the teacher (me) unless I move into the view of the camera, usually at the behest of the students featured. These tapes, then, present a very particular view of the classroom. The viewer is necessarily drawn into the experience of the students featured on the tapes, for there is little else on which to focus one’s eyes and ears. Fennema et al. (1996) and Steinberg, Empson, and Carpenter (2004) note that there is increasing evidence that knowledge of children’s thinking is a powerful influence on practising teachers as they consider instructional change, and Bennett and Jacobs (1998) and Vacc and Bright (1999) make similar claims for beginning teacher education following their studies of preservice teachers’ responses to courses designed to help beginning teachers to construct a framework for understanding children’s mathematical thinking. Such evidence suggests that knowledge of children’s thinking might be significant in breaking the chain of preservice teachers’ dependence on a teacher-focused orientation to teaching. That the preservice teachers in this study show a marked willingness to engage in explorations of student thinking in preference to (or at least before) an exploration of teacher actions is therefore significant, and suggests that video excerpts that focus on the learner not the teacher offer potential for supporting the re-orienting of beginning-teacher thinking.

The following example highlights preservice teachers’ responses to a video featuring a pair of Grade 6 students who were members of one of my high-school classes at a time when I was a full-time teacher of mathematics (simultaneously researching my own practice) in a small, rural secondary school in the UK³. The video shows the children trying to find the perimeter of the plane figure shown in Figure 1.

Figure 1. Plane figure

The two students work for a time, then call for help from me, their teacher, and eventually produce the following expression for the perimeter⁴: 41 - (1c + 1b) + 3 + 1b + 1c. Asking the question, “Is their answer correct?” tends to provoke some discussion amongst both preservice and practising teachers. Asking, “Is their answer correct enough?” often provokes a heated exchange or a contribution that reveals a concern with the fact that this un-simplified expression reveals a lack of student understanding of the rules of algebra, even while it represents a ‘correct’ method for finding the perimeter and involved some fairly sophisticated use of algebra for Grade 6 students (including the assigning of a value of 12-(b + c) for the length of the ‘missing’ horizontal line segment.) Here are two examples of preservice teachers’ responses to my probing about whether the above formula is ‘correct enough’:

Notice above the different foci preservice teachers Liz (lines 1-9) and Elle (line 10) have in response to the two Grade 6 students’ problem-solving efforts. Here we can see that Liz focuses on the details of the students’ actual solution while Elle shows concern about the ‘big picture’ in terms of the (lack of) sophistication of their strategy. Paying attention to such differences in preservice teachers’ preoccupations when analysing student learning is helpful to me as a teacher educator as I choose follow-up video examples and as I structure other learning tasks intended to occasion each individual preservice teacher’s growth.

The Role of Video in Fostering Reflection on Teaching

It has been my experience that when the beginning teachers do turn their attention away from student learning and towards the teaching, as they inevitably will, any question or comment that might be construed as critical of the teacher (who it should be remembered is, in this case, also their university tutor) sometimes comes cautiously, though as Noah’s critiques below show (lines 12 and 14), my students were also astute (and pithy) in their observations. When beginning teachers seem over-cautious in airing their critiques, I make explicit my stance on this matter—that I wholeheartedly encourage their critique and value their inquisitive questions. And I tell them why—because such challenges provoke me to reflect more deeply on my beliefs about teaching and learning. In this way I hope that seeds are sown in the quest to foster reflection on practice. However, beginning teachers will only be comfortable critiquing the classroom practice of their university tutor if they can be assured that such critique will be welcomed in the spirit in which it is offered. I tend to introduce video extracts only after I have established a good working relationship with my students, and after they have heard me (more than once) reflect openly on problematic areas of my own practice.

As is evidenced below, critiques of my teaching also offer me the opportunity to remind students of the huge diversity of student experience and competence they will encounter (lines 25–27), and the opportunity to describe effective teaching strategies (line 28).

The following extract reveals preservice teachers’ responses to a videotape featuring two Grade 6 students in my own high-school classroom working on a problem that integrated geometric and algebraic reasoning. The original problem posed to the Grade 6 class had been to find an algebraic generalisation for the number of one-unit-square paving stones needed to surround a square pond of any size (see Figure 2).

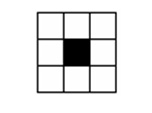
Figure 2 . Square pond

During the lesson, several Grade 6 students had accomplished this task much more quickly than I, as their teacher, had expected, and so we had extended the problem to consider rectangular ponds (see Figure 3) and, over successive lessons, L-shaped ponds, triangular ponds surrounded by triangular paving stones, and 3-D versions of the problem.

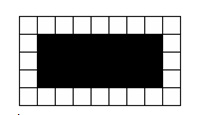
Figure 3. Rectangular pond

In the videotape episode I showed to my preservice teachers, the Grade 6 students, Kayleigh and Carrie, could be observed developing an algebraic generalisation for the number of one-unit-square paving stones needed to surround a rectangular pond of width w and length n. Their final written expression, 2n + (2w + 2), is mathematically incorrect (it should be 2n + 2(w + 2)), but their verbal description of the process (take the width, add two on to it, double it because it’s got two ends, and then add on two lots of the length) is correct. As their teacher, on the videotape I can be observed agreeing with their process but, unable to ignore the incorrect expression, I had added a set of parentheses into their expression to correct the mathematics: 2n + (2(w + 2)). In my university classroom I stopped the videotape at this point, leaving some ambiguity about whether I was about to walk away from the students on the video or follow up with further instructions, and this seemed to prompt a question from Noah, an elementary-route preservice teacher, about me leaving (line 12), which he then followed up with a strong critique of my teacherly focus on a final correct answer (lines 12 and 14), a critique that I embraced (line 18). This seemed to prompt Noah to go further to explore my ‘state of mind’ or ‘teacher thinking’ about the incident (line 19):

As the class with the preservice teachers continues I describe the importance of task structure in helping not only to teach important content but in ensuring that all students learn:

As can been seen from the above transcript, the very presence of the teacher who was featured on the video during the discussion of the video extract can, in addition to serving as a space to reflect on teaching, also facilitate a re-focusing on the learner. Here, although the preservice teacher, Noah (line 19), inquired about teacher thinking, the teacher re-focused attention on the learners (lines 25–27) by drawing attention to the fact that her thinking was about the learners and their various growing capabilities (not about, for instance, ‘covering’ the curriculum), and then by offering strategies for encouraging learning (line 28).

The Role of Video in Offering Possibilities for Imaginative Rehearsal

One issue that has arisen for me in my use of video in teacher education is the potential that my videos hold for provoking a feeling of inadequacy in my students. One of the things I have on occasion done is to stop the tape at a particular point and ask students what they think happens next (with respect to a number of different viewpoints such as a child’s potential reaction to an instruction, or the teacher’s potential response to a student’s question). I do this not so that my students have to play a guessing game to which I already know the answer (though I am aware of the potential for this reading), but so that they might be encouraged to anticipate the potential complexity of the situation as they hear their colleagues’ suggestions. Such deliberation “is actually an imaginative rehearsal of various courses of conduct” (Dewey, 1908/1932, p. 303) and therefore such moments also offer the students a space in which to reflect on how they might respond in a similar situation, however, as this approaches a form of role-playing and focuses them closely on the teacher (a tendency about which I have already expressed concern) I am cautious in its use. The ‘what happens next’ strategy, then, can be both powerful and threatening. It is powerful in that the beginning teachers can feel validated when they suggest a potential strategy for the teacher that they subsequently see enacted on the videotape (especially if the strategy seems effective). It also holds power in its ability to expand beginning teachers’ conceptions of what children are capable of doing with and through mathematics (for instance, my elementary preservice teacher education students have often expressed surprise at the level of mathematical sophistication of some of the Grade 6 children on the tapes), and it holds power in its ability to broaden beginning teachers’ perceptions of how a (seemingly) simple question, problem or instruction can be variously interpreted by children.

The ‘what happens next’ technique becomes threatening, however, either when the strategy that a teacher education student suggests happens to be the one enacted by the teacher on the tape but it is seen to provoke confusion or lack of understanding for the children, or when the beginning teacher’s classmates (with encouragement from me) begin to unpack and critique the teaching on the tape—however effective it may have seemed at first glance. In fact, the ‘what happens next’ becomes particularly problematic when a strategy is suggested that appears on tape to be successful at that moment, but which, from my one-step-removed perspective, I now critique. Because I am apt to critique my own teaching quite vigorously, beginning teachers can be left wondering whether there is any approach that would satisfy me, and I sometimes fear that this makes them feel that the whole enterprise of teaching is too complex, too difficult, for them ever to learn to do well. I try to balance my critique of my own teaching with expressions of the joy I feel when teaching and things are going well, but I remain cautious of my power to demoralise beginning teachers and therefore cautious in my use of the ‘what happens next’. Nevertheless, it is a seductive game for video, somehow made all the more tempting when one has in one’s hand a remote control pad that can freeze a picture in the blink of an eye and leave an expression, a word, or a gesture hanging (sometimes literally) in the air, begging for resolution.

Here is one example of preservice teachers’ responses to my use of a role-playing “what would you do?” or “what do you think happens next?” type of strategy. This excerpt is also taken from data concerning preservice teachers’ responses to the videotaped Grade 6 ‘Ponds’ lesson described in the previous section. However, this excerpt is from slightly earlier in the preservice teachers’ session where they had been watching an earlier part of the Grade 6 videotape⁶. The Grade 6 students on the videotape have been working on generalising the number of square paving stones needed to surround a rectangular pond of any size (see Figure 3 for an example of a ‘pond’ and surrounding paving stones that was offered to the Grade 6 students). The two students on whom the video focuses throughout the lesson in question have developed a table of data (Figure 4) and a formula (2n + 10) which, although it correctly represents the successive numbers of paving stones that would be needed to surround the ‘family’ of ponds (with fixed width three) shown in Figure 5, does not match their data table (Figure 4) and, crucially, does not account for the two variables of length and width of any rectangular pond.

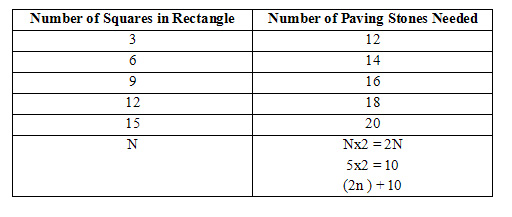
Figure 4. Students’ data chart

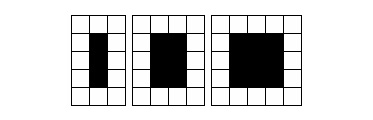
Figure 5. Family of rectangular ponds of fixed width three units

Notice in particular here that although I frame a question that one might expect would orient preservice teachers to the role of the teacher (“As the teacher, what do you do with this?”), their instinct is to first take up the student thinking they have observed, a response that I suggest is partly occasioned by the focus of the video camera being firmly on the two students rather than on the teacher:

The preservice teachers’ responses reflect a myriad of concerns. Nicole (line 30), Jeanette (line 42), and Liz (line 48) exhibit concerns about the correctness of the mathematics. Deepak (line 46) exhibits an interest in excavating beneath students’ written expressions of understanding, rather than simply listening in order to correct errors—a common teacher flaw ( Davis, 1996). Noah (lines 36 and 38), Nicole (line 40), and Heather (line 49) offer proposals for how the students may have interpreted the problem, and Noah (line 34), Deepak (lines 46 and 54), and Liam (line 57) offer possible courses of action for the teacher. The apparent disadvantage of videotape use—that the “what happens next” game can be a threatening one—can also, then, be seen in a positive frame, allowing preservice teachers both to explore possibilities for gaining understanding of student thinking and to rehearse possibilities for action.

Discussion

The Role of Videotape in Drawing Viewers Close to the Complexities of Teaching and Learning

My work has shown that video extracts have the power to draw viewers close to the complexities of teaching and learning in classrooms, whilst releasing the viewer from the concern of having to attend to all that is happening in the classroom. Structured practicum experiences that allow beginning teachers initially to work with part of a class rather than the whole class, or that allow for co-teaching in a beginning teacher’s early experiences, offer similar opportunities for release from the concerns of managing a class of learners, and are certainly valuable, however, such experiences are not always supported by the extended explorations that are possible with the use of videotaped episodes, and are not usually common experiences for all of the group. In offering preservice teachers the experience of exploring my teaching, I am offering a common experience or ‘text’ that can be returned to throughout the semester, a feature of teacher education that Darling-Hammond et al. (2005, p. 408) and Lampert and Ball (1998, p. 41) suggest is important in helping preservice teachers learn to analyse teaching and connect theory and practice and that Masingila and Doerr (2002, p. 257) suggest enables preservice teachers to analyse pedagogical issues in a way that takes them beyond the usual concerns of classroom management and into more complex issues of practice. In addition, from my perspective,such practices model the art of reflecting on teaching and emphasise the importance of continuing to perceive oneself as a learner throughout one’s teaching career.

The complexity offered by videotape also presents problems for me as a teacher educator though, as I struggle to make choices about how to structure the video-based classes, how to assess what and whether the preservice teachers are learning, whether to re-direct the conversation, when to move on to a new extract or to another activity altogether, and whether to share these anxieties with the class. As this list of my struggles seems to closely resemble a list which might be drawn up to represent the struggles that many preservice teachers go through in learning to teach, I am able to make explicit to the preservice teachers what it is that I think I am learning from our interactions, thereby reinforcing my positioning as a learner as well as a teacher.

Final Remarks

Though not all teacher educators have access to recordings of their own elementary or high school teaching, I strongly recommend the use of the technique I have described here wherever possible. I also hope that more teacher educators will embark upon the kinds of projects that researchers such as Lampert and Ball (1990, 1998) and Simmt (2002, 2003a, 2003b, 2003c) have initiated, whereby relationships are established with schools which allow university-based educators to teach in those schools and to record their experiences for use in teacher education. My own experience has shown that use of videotaped materials that feature a university instructor’s own school teaching can be a powerful intervention in teacher education. The opportunity to analyse lessons with the teacher who taught them seems to be a particularly significant event for many preservice teachers. Having said this, many of the advantages I have outlined may also be experienced through appropriate use of videotapes of teaching from other sources. In particular, through the use of video extracts that focus closely on a small group of learners, preservice (and practising) teachers are released to consider at length the mathematical understandings of just a few students, a privilege they are not normally afforded when in a practicum (or full-time teaching) situation, and such considerations encourage preservice and practising teachers to be interested in how students learn, not simply in how they should be taught. Such a re-orientation is important in fostering practical wisdom in teaching, wherein good judgement matters and praxis, or thoughtful action, is encouraged. Enacted in the ways described here, pedagogical strategies that incorporate the use of classroom video can participate in the shaping of new orientations to teaching.

Acknowledgements

Artzt, A., & Armour-Thomas, E. (1992). Development of a cognitive-metacognitive framework for protocol analysis of mathematical problem solving in small groups. Cognition and Instruction, 9(2), 137–175.

Ball, D. (1988). Unlearning to teach mathematics. For the Learning of Mathematics, 8(1), 40–48.

Ball, D. (1990). Breaking with experience in learning to teach mathematics: The role of a preservice methods course. For the Learning of Mathematics, 10(2), 10–16.

Ball, D. (1995). Developing mathematics reform: What don’t we know about teacher learning – but would make good working hypotheses? Craft Paper 95–4. Michigan State University, East Lansing, MI: National Center for Research on Teacher Learning.

Ball, D. (2000). Working on the inside: Using one’s own practice as a site for studying teaching and learning. In A. Kelly & R. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 365–402). Mahwah, NJ: Lawrence Erlbaum.

Ball, D., & Cohen, D. (1999). Developing practice, developing practitioners: Toward a practice-based theory of professional education. In L. Darling-Hammond & G. Sykes (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 3–32). San Francisco: Jossey-Bass.

Bennett, T., & Jacobs, V. (1998, April). Becoming a teacher of mathematics: The effects of a children’s thinking approach. Paper presented at the annual meeting of the American Educational Research Association. San Diego, CA.

Bottorff, J. (1994). Using videotaped recordings in qualitative research. In J. Morse (Ed.), Critical issues in qualitative research methods (pp. 244–261). Thousand Oaks, CA: Sage.

Britzman, D. (1991). Practice makes practice: A critical study of learning to teach. Albany, NY: State University of New York Press.

Burnard, P., Craft, A., Cremin, T., Duffy, B., Hanson, R., Keene, J., et al. (2006). Documenting “possibility thinking”: A journey of collaborative enquiry. International Journal of Early Years Education, 14(3), 243–262.

Calderhead, J. (1981). Stimulated recall: A method for research on teaching. British Journal of Educational Psychology, 51, 211–217.

Coulter, D., & Wiens, J. R. (2002). Educational judgement: Linking the actor and the spectator. Educational Researcher, 31(4), 15–25.

Darling-Hammond, L., Hammerness, K., Grossman, P., Rust, F., & Shulman, L. (2005). The design of teacher education programs. In L. Darling-Hammond & J. Bransford (Eds.), Preparing teachers for a changing world. What teachers should learn and be able to do (pp. 390–441). San Francisco: Jossey-Bass.

Davis, B. (1996). Teaching mathematics: Toward a sound alternative. New York: Garland Publishing.

Dewey, J. (1932). Ethics. (J. Dewey & J. Tufts, Eds.) (Rev. ed.). New York: Henry Holt & Co. (Original work published in 1908)

Doerr, H., & Thompson, T. (2004). Understanding teacher educators and their preservice teachers through multi-media case studies of practice. Journal of Mathematics Teacher Education, 7(3), 175–201.

Dunne, J. (1997). Back to the rough ground. Practical judgement and the lure of technique. Notre Dame, IN: University of Notre Dame Press.

Dunne, J. (2005). An intricate fabric: Understanding the rationality of practice. Pedagogy, Culture and Society, 13(3), 367–389.

Dunne, J., & Pendlebury, S. (2002). Practical reason. In N. Blake, P. Smeyers, R. Smith, & P. Standish (Eds.), The Blackwell guide to the philosophy of education (pp. 194–211). Oxford, UK: Blackwell.

Fennema, E., Carpenter, T., Franke, M., Levi, L., Jacobs, V., & Empson, S. (1996). A longitudinal study of learning to use children’s thinking in mathematics instruction. Journal for Research in Mathematics Education, 27(4), 403–434.

Flyvbjerg, B. (2001). Making social science matter: Why social inquiry fails and how it can succeed again. Cambridge, UK: Cambridge University Press.

Gauthier, C. (1992). Between crystal and smoke. Or, how to miss the point in the debate about action research. In W. Pinar & W. Reynolds (Eds.), Understanding curriculum as phenomenological and deconstructed text. New York: Teachers College Press.

Giudici, C., & Rinaldi, C., & Krechevsky, M. (Eds.). (2001). Making learning visible: Children as individual and group learners. Cambridge, MA: Reggio Children/ Harvard Project Zero.

Goldman-Segall, R. (1993). Interpreting video data: Introducing a “significance measure” to layer description. Journal of Educational Multimedia and Hypermedia, 2(3), 261–281.

Goldman-Segall, R. (1998). Points of viewing children’s thinking: A digital ethnographer’s journey. Mahwah, NJ: Lawrence Erlbaum.

Harvard Project Zero. (2003). Making teaching visible: Documenting individual and group learning as professional development: A Making Learning Visible monograph. Cambridge, MA: Harvard Project Zero.

Howey, K., & Zimpher, N. (1999). Pervasive problems and issues in teacher education. In G. Griffin (Ed.), The education of teachers. 98 th Yearbook of the National Society for the Study of Education (pp. 279–305). Chicago: Chicago University Press.

Huinker, D., & Freckmann, J. (2004). Focusing conversations to promote teacher thinking. Teaching Children Mathematics, 10(7), 352–357.

Jaworski, B. (1989). Using classroom videotape to develop your teaching. Informal publication. Milton Keynes, UK: Centre for Mathematics Education, The Open University.

Lampert, M., & Ball, D. (1990). Using hypermedia technology to support a new pedagogy of teacher education. Issue Paper 90-5. East Lansing, MI: National Center for Research on Teacher Learning.

Lampert, M., & Ball, D. (1998). Teaching, multimedia, and mathematics: Investigations of real practice. New York: Teachers College Press.

Lampert, M., & Ball, D. (1999). Aligning teacher education with contemporary K-12 reform visions. In L. Darling-Hammond & G. Sykes (Eds.), Teaching as the learning profession: Handbook of policy and practice (pp. 33–53). San Francisco: Jossey-Bass.

Lund , D., Panayotidis, L., Smits, H., & Towers, J. (2006). Fragmenting narratives: The ethics of narrating difference. Journal of the Canadian Association of Curriculum Studies, 4(1), 1–23.

Lund , D., Panayotidis, L., Smits, H., & Towers, J. (2007, February). Provoking and being provoked by the senses: Listening, speaking, seeing, and feeling (through) inquiry in teacher education. Paper presented at the Canadian Association of Curriculum Studies ‘Provoking Curriculum’ Conference. Banff, AB. February, 2007.

Maher, C. A. (2002). How students structure their own investigations and educate us: What we’ve learned from a fourteen year study. In A. D. Cockburn, & E. Nardi (Eds.), Proceedings of the twenty-sixth annual meeting of the International Group for the Psychology of Mathematics Education (Vol. 1, pp.31–46). Norwich, UK: School of Education and Professional Development, University of East Anglia.

Marland, P. (1984). Stimulated recall from video: Its use in research on the thought processes of classroom participants. In O. Zuber-Skerritt (Ed.), Video in Higher Education (pp. 226–237). London: Kogan Page.

Martin, L. C. (1999). The nature of the folding back phenomenon within the Pirie-Kieren Theory for the growth of mathematical understanding and the associated implications for teachers and learners of mathematics. Unpublished doctoral dissertation, Oxford University.

Masingila, J., & Doerr, H. (2002). Understanding pre-service teachers’ emerging practices through their analyses of a multimedia case study of practice. Journal of Mathematics Teacher Education, 5(3), 235–263.

Merseth, K. (1993). How old is the shepherd? An essay about mathematics education. Phi Delta Kappan, March, 548–554.

Niguidula, D. (2005). Documenting learning with digital portfolios. Educational Leadership, 63(3), 44–47.

Phelan, A. (2005). On discernment: The wisdom of practice and the practice of wisdom in teacher education. In G. F. Hoban (Ed.), The missing links in teacher education design: Developing a multi-linked conceptual framework (pp. 57–73). Dordrecht, The Netherlands: Springer Press.

Pimm, D. (1993). From should to could: Reflections on possibilities of mathematics teacher education. For the Learning of Mathematics, 13(2), 27–32.

Pirie, S. E. B. (1996). What are the data? An exploration of the use of video-recording as a data gathering tool in the mathematics classroom. In E. Jakubowski, D. Watkins, & H. Biske (Eds.), Proceedings of the annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Vol. II (pp. 553–559). Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.

Pirie, S. E. B. (1998). Where do we go from here? In A. R. Teppo (Ed.), Qualitative research methods in mathematics education (Monograph No. 9, pp. 156–163). Reston, VA: National Council of Teachers of Mathematics.

Pirie, S. E. B. (2001). Analysis, lies, and videotape. In R. Speiser, C. A. Maher, & C. N. Walter (Eds.), Proceedings of the Twenty-Third Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Snowbird, Utah) (Vol. I, pp. 346–350). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.

Pirie, S. E. B, & Kieren, T. E. (1994). Beyond metaphor: Formalising in mathematical understanding within constructivist environments. For the Learning of Mathematics, 14(1), 39–43.

Powell, A. B., Francisco, J. M., & Maher, C. A. (2003). An analytical model for studying the development of learners’ mathematical ideas and reasoning using videotape data. Journal of Mathematical Behavior, 22, 405–435.

Prosser, J. (2000). The moral maze of image ethics. In H. Simons & R. Usher (Eds.), Situated ethics in educational research (pp. 116–200). London: Routledge.

Ricoeur, P. (1992). Oneself as another (Kathleen Blamey, Trans.). Chicago: University of Chicago Press.

Selinger, M. (1994). Responses to video in initial teacher education. In P. da Ponte & F. Matos (Eds.), Proceedings of the eighteenth annual meeting of the International Group for the Psychology of Mathematics Education, Vol. IV, (pp. 241–248). Lisbon, Portugal.

Simmt, E. (1996, April). Children and parents and mathematics: Occasioning in mathematical cognition. Paper presented at the annual meeting of the American Educational Research Association. New York.

Simmt, E. (2002). The confessions of a mathematics education professor. Presentation at the annual conference of the Mathematics Council of the Alberta Teachers’ Association. Canmore, AB.

Simmt, E. (2003a). Mathematical extra-sensory perception or mathematical reasoning? Delta-K, 40(1), 20–22. Edmonton, Alberta: Alberta Teachers’ Association.

Simmt, E. (2003b). Personalizing tests and quizzes. Paper presented at the Canadian Regional Conference of the National Council of Teachers of Mathematics. Edmonton, AB.

Simmt, E. (2003c). Dividing fractions. Workshop presented at the Canadian Regional Conference of the National Council of Teachers of Mathematics. Edmonton, AB.

Smits, H. (1997). Hermeneutically-inspired action research: Living with the difficulties of understanding. Journal of Curriculum Theorizing, 13(1), 15–22.

Smits, H., Wang, H.C., Towers, J., Crichton, S., Field, J., & Tarr, P. (2005). Deepening understanding of inquiry teaching and learning with e-portfolios in a teacher preparation programme. Canadian Journal of Learning and Technology, 31(3), 111–119.

Steinberg, R., Empson, S., & Carpenter, T. (2004). Inquiry into children’s mathematical thinking as a means to teacher change. Journal of Mathematics Teacher Education, 7(3), 237–267.

Sykes, G., & Bird, T. (1992). Teacher education and the case idea. Special Report Number 8/92. East Lansing, MI: National Center for Research on Teacher Learning.

Szente, J., Massey, C., & Hoot, J. (2005). Eyes in the back of your head: Cameras for classroom observation. Learning and Leading with Technology, 32(5), 18–21.

Towers, J. (1996a). False impressions: Listening for understanding in the mathematics classroom. In E. Jakubowski, D. Watkins, & H. Biske (Eds.), Proceedings of the eighteenth annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Vol. II (pp. 527–532). Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education.

Towers, J. (1996b). When silence says it all: An exploration of students’ mathematical talk. In Y. Pothier (Ed.), Proceedings of the annual meeting of the Canadian Mathematics Education Study Group/Groupe Canadien d’Etude en Didactique des Mathematiques (pp. 151–156). Halifax, Nova Scotia: Mount Saint Vincent University.

Towers, J. (2007a). Living ethically in the classroom: Enacting and sustaining inquiry. Manuscript submitted for publication.

Towers, J. (2007b) Feeling prepared and being prepared: A case study of learning to teach (through) inquiry. Manuscript submitted for publication.

Towers, J., & Martin, L. C. (2007). The emergence of a ‘better’ idea: Preservice teachers’ growing understanding of mathematics-for-teaching. Paper presented at the annual meeting of the American Educational Research Association. Chicago, IL. April 2007.

Vacc, N., & Bright, G. (1999). Elementary preservice teachers’ changing beliefs and instructional use of children’s mathematical thinking. Journal for Research in Mathematics Education, 30(1), 89–110.

Wall, J. (2003). Phronesis, poetics, and moral creativity. Ethical Theory and Moral Practice, 6, 317–341.

Wilson , S. (1990). The secret garden of teacher education. Phi Delta Kappan, Nov, 204–209.

Wood, T., Cobb, P., & Yackel, E. (1991). Change in teaching mathematics: A case study. American Educational Research Journal, 28(3), 587–616.

Footnotes

* An earlier version of this paper was presented at the 1998 annual meeting of the American Educational Research Association, San Diego, CA.

2 Part of my ongoing interest is in how students come to understand the mathematics they are studying, which is why I choose to focus on the conversations and actions of pairs or small groups of students rather than capture a wider (but more general) view of the classroom. The students were all volunteers and represented the breadth of ability levels, socioeconomic status, gender, race, etc. of the high-school students I taught during the period of data collection.

3 The age of the children corresponds to a Grade 6-equivalent in North America, though in the UK this grade level is referred to as ‘Year 7’ and is a secondary-school grade. For ease of reference here, the children will be referred to as Grade 6 throughout.

4 I detail elsewhere how this answer was obtained (Towers, 1996b). Briefly, it involved the students assigning values to the ‘missing’ line segments (3 for the vertical and 12 - (b + c) for the horizontal) and then adding all the line segments together).

5 Pseudonyms are used throughout to identify preservice teachers and school children.

6 For ease of reference in this article, transcript lines have been numbered chronologically as they are presented in the text, however, extract 29–59 is actually from an earlier part of the university class than extract 11–28.

© Canadian Journal of Learning and Technology

ISSN: 1499-6685