Authors
Qing Li is an Associate Professor in the Faculty of Education, University of Calgary. Correspondence regarding this article can be sent to her at: Qinli@ucalgary.ca
Abstract: This study examines possible interaction effects of gender and region (urban vs. rural) on student beliefs about women in math and science, their attitudes towards math and science, and their confidence in the use of technology. A secondary purpose of this study is to examine possible differences in confidence of using technology between high school students who consider math-related or science-related careers and those who do not. The data collected from an anonymous survey of 450 secondary students were analyzed. The results showed interaction effects of gender and region on student beliefs and attitudes. First, the gender differences in students’ beliefs about women in math and science changes significantly depending on the location of the school. Second, when region was considered, significant effects on students’ choice of mathematics- and science-related careers were identified. Urban students, regardless of their gender, were more likely to consider careers related requiring knowledge of science or mathematics than rural students.
Résumé : Cette étude examine les effets d’interaction possibles du genre et de la région (la ville ou la banlieue) sur les croyances des étudiants à propos des femmes dans le domaine des mathématiques et des sciences, leurs attitudes envers les mathématiques et les sciences et leur confiance en l’utilisation de la technologie. Un objet secondaire de cette étude consiste à examiner les différences possibles en la confiance en l’utilisation des technologies entre les étudiants du secondaire qui envisagent des carrières dans le domaine des mathématiques ou des sciences et entre les étudiants pour qui ce n’est pas le cas. Nous avons analysé les données recueillies dans le cadre d’un sondage anonyme effectué auprès de 450 étudiants du secondaire. Les résultats ont indiqué des effets d’interaction du genre et de la région sur les croyances et les attitudes des étudiants. Tout d’abord, les différences de genre chez les croyances des étudiants relatives aux femmes en mathématiques et en sciences changent grandement selon l’emplacement de l’école. Ensuite, lorsqu’on tient compte de la région, nous avons observé des effets importants sur le choix par les étudiants de carrière en mathématiques ou en sciences. Les étudiants des villes, peu importe leur genre, envisagent plus souvent des carrières dans les domaines des sciences ou des mathématiques que les étudiants des banlieues.
Because of the belief that there should be equity for females and males in education, educational issues related to gender are actively researched in many countries (King & McLeod, 1999) and have been studied intensively for about three decades (Fennema, 2002; Fennema, Carpenter, Jacobs, Frank, & Levi, 1998; Francis, 2000) . The research results have stimulated many efforts to improve educational practices for all students in schools. Although schools are making progress toward equitable treatment of male and female students, concerns remain (American Association of University Women, 1999) . In its 1999 report, the American Association of University Women (AAUW) states that in mathematics and science, male students still outscore female students and the gender gap increases with grade level on nationally and internationally representative tests such as SAT and TIMSS. Although technology is expected to “bridge the educational gap between wealthy and poor students, little attention has been given to how computer technology is affecting the educational gap between girls and boys” (AAUW, p. 10). The report further indicates that, despite the dramatic entry of the Internet into our schools in the past several years, technology is beginning to create a new gender gap (American Association of University Women, 1999) .
The persistent gender gap identified in mathematics, science, and the emerging gender disparities in technology are complicated by other factors such as inequalities of region. For instance, rural students are at a higher risk of leaking out of the science and mathematics pipeline because of low resource availability and poor visibility (Schoenfeld, 2002) . While many, if not most, rural schools have basic Internet access, they remain, as a rule, technologically impoverished (Li & Willing, 2002) .
This inequity calls for action on the part of educators, researchers, policy makers and the like. Before we can tackle the problem, however, a thorough understanding of the issues is necessary. It is essential to examine the effects of gender, region, and other factors on student learning to deepen our understanding of the complicated issue of the inequality identified in mathematics, science, and technology. This study, therefore, explores the effects of gender, region, and race on student beliefs and attitudes related to mathematics, science, and technology from a multivariate analytical perspective.
The main purpose of this study is to examine possible interaction effects of gender and region on student beliefs about women in math and science, their attitudes toward mathematics and science, their confidence in using technology, as well as their beliefs about the effectiveness of technology in learning. Specifically, to what extent do gender and region affect students’ beliefs about women in mathematics and science as well as their attitude toward learning mathematics and science, and their confidence in using technology?
The focus then moves to students’ career considerations and the effectiveness of technology for learning: Do male and female students differ in their career considerations and beliefs about the effectiveness of technology in learning? Do urban and rural students differ in their career considerations and beliefs about the effectiveness of technology in learning?
The secondary purpose of this study is to identify possible patterns of students’ career considerations and their confidence in using technology. Specifically, is there a difference in confidence in using technology between high school students who consider math-related or science-related careers and those who do not?
Research on gender-related differences and affective variables in mathematics and science education has been conducted from a variety of perspectives. Although these research studies have encouraged efforts to improve educational practices for all students in schools and some studies have shown a narrowing trend in the gender gap over time (Connolly, Hatchetter, & McMaster, 1999; Hyde, Fennema, & Lamon, 1990) , gender inequity remains a serious concern. For example, it was found that significant differences in achievement in mathematics and science appear by later adolescence and the gender gap increases with the grade level (Ambrose, Levi, & Fennema, 1997; American Association of University Women, 1999) . Females continue to opt out of mathematics and science in the later stages of their educational careers (Arnot, Gray, James, Rudduck, & Duveen, 1998) . Some studies even showed significant gender differences in problem-solving strategies starting as early as Grade 1 (Carr, Jessup, & Fuller, 1999; Fennema et al., 1998) . Similar trends were identified in the use of technology. As summarized by Fennema (2002), the gender problem in mathematics and science “still exists in much the same form that it did in 1974.”
The most representative and comprehensive examination of students’ learning of mathematics and science across national boundaries is the Third International Mathematics and Science Study (TIMSS) (Mullis et al., 2000) . It is the largest of the international comparative studies involving more than half a million students in 41 countries. The TIMSS report of the International Association for the Evaluation of Educational Achievement (IEA) revealed that, in most countries, males had significantly higher average marks than females in both mathematics literacy and in advanced mathematics in the final years of secondary school. In Grades 4 and 8, the few statistically significant differences that were identified favoured males over females. In science, gender inequality was even more pronounced than in mathematics. Significant gender differences were found in science achievements in half of the TIMSS countries, including the US and Canada. In the fourth grade, the differences favouring males in science were substantially more pronounced than in the TIMSS mathematics results. When different content areas were scrutinized, many significant differences favouring males were found, particularly in earth science and physical science. In many countries, eighth grade males scored significantly higher than females in various science subjects, particularly in earth science, physics, and chemistry. In the final year of secondary school, almost all countries showed statistically significant gender differences in science literacy in favour of males. In a nutshell, although the gender differences in achievement vary depending upon the particular science or content area, the general pattern is that the significant differences often favour males over females in the three grades examined.
Students’ attitudes and beliefs have a strong impact on their performance in a particular subject area, so TIMSS collected data regarding student beliefs about the importance of mathematics and science. The data showed a progression from the fourth grade (more females than males felt it was important to do well in mathematics and science) to the eighth grade (few differences by gender), to the twelfth grade, when significantly more males than females in most countries reported that it was important to do well in mathematics and science.
When parents were considered, the data showed a significant gender difference in parental views about the importance of learning mathematics and science. As early as the eighth grade, more males than females in nearly every country strongly agreed that it was important to do well in mathematics to please their parents.
Do males and females differ in their views about future careers related to mathematics and science? In many of the TIMSS countries, significant gender differences were identified. For example, as early as the eighth grade, more males than females reported that doing well in mathematics was important for getting a desired job, while females in the majority of the countries disagreed or strongly disagreed about the importance of future employment as a reason to do well in mathematics. A similar pattern was identified for science, with significantly more males than females internationally reporting that doing well in science was important to getting a desired job, and significantly more females than males disagreeing or strongly disagreeing about the importance of future employment as a reason to do well in science. For twelfth graders, significantly more males than females wanted a mathematics- or science-related job; whereas about three-fourths of the females did not want a job that involved the use of mathematics or science.
The gender pattern observed internationally was also reflected in North America: female and male students had comparable levels of interest and achievement in math, science, and technology in early elementary grades (McLester, 1998) . This slowly changed in upper elementary and the gender gap in mathematics and science became significant in senior high when a disproportionate number of females drops out of advanced mathematics and science (Ma, 1999) . Similarly, significant gender inequality started to appear in middle school when females were more likely to view the computer as a tool to complete a task, whereas males played games and established a “friendship” with their computer (Fiore, 1999) .
This gender disparity widens in post-secondary school. Although the enrolment in computer science is decreasing in general, the number of females who choose a career in computer science has significantly decreased compared to males. Females remain underrepresented in fields with the highest salaries, including math, science, and technology, even though they represent half the work force and earn more than half the current bachelor’s degrees (American Association of University Women, 2000) .
[T]he lack of technological literacy on the part of women is anything but harmless. It bolsters job segregation and all the economic disadvantages this implies in an increasingly mechanized world, including differential earnings and power. Women are seldom employed in occupations that require technological expertise. (Leonard, 2003, p. 233)
Further, research evidence indicates that this gender inequity favouring male learning is affected by other variables including region and race. Previous research documented significant regional differences in mathematics and science, arguing that rural students are at a higher risk for leaking out of the science and mathematics pipeline (Schoenfeld, 2002) . In addition, it was claimed that rural schools lag behind in technology because of the economic disadvantages of the community (Li & Willing, 2002) . Although inner city urban schools may have similar challenges, the rural schools, in general, are significantly disadvantaged in technology compared to their urban counterparts (Hudson & Shafer, 2004) . Research showed that
[technology] has become a major instrument of elite male domination in terms of education, role, models, and job opportunities.…Women are socially conditioned to avoid technology. Women of colour have been segregated into labour-intensive, low technology employment…[and they] remain located in the more traditional, less-skilled occupations. (Leonard, 2003, p. 55)
In short, mathematics, science, and technology are rooted in power inequalities and the benefits are structurally patterned by gender, race in our society and beyond (Benskin, 1994; Fennema, 2002; Leonard, 2003) . While jobs requiring science, math and technological skills are growing at nearly double the rate of all jobs, women and people of colour are still significantly under-represented in fields requiring advanced degrees in math and science. (Mid-Atlantic Equity Consortium, n.d.) .
Research studies have documented a number of important factors contributing to this gender gap. These factors included: student attitudes (Karp, 1998) , self-efficacy (Bong, 1999) , self-confidence (Sanders & Peterson, 1999) , parental involvement (Ma, 1999) , teacher attention (Sadker, 1999) , textbook content (Parker, 1999) , knowledge of future careers (Lightbody & Durndell, 1996; Rohrer & Welsh, 1998) .
Many research studies suggest that mathematics, science, and technology are a “critical filter” for students’ future development. The well-documented, persistent gender gap in mathematics and science, coupled with the emerging gender inequity in technology, call for further exploration of gender issues in these areas. While there appears to be consensus that gender disparity occurs in mathematics, science, and technology, limited research has been conducted to examine other forms of inequality, such as region and race (Leonard, 2003) . Of that limited offering, even fewer have addressed gender differences interacting with other factors like region and race. This study, therefore, examines secondary students’ beliefs and attitudes in relation to mathematics, science, and technology, considering the interactive effects of gender, region, and race from a multivariate analytical perspective.
The participants were 450 (207 male, 236 female) Grade 7–12 students randomly chosen from two urban and two rural schools in Alberta, Canada. There were 351 students from urban schools and 92 students from rural schools. A total of 72.7% of students were Caucasians and 27.3% students of Asian, Aboriginal and other ethnicity. Most of the students of Asian, Aboriginal and other ethnicity were located in urban schools. Only 2.4% of rural students were non-Caucasians.
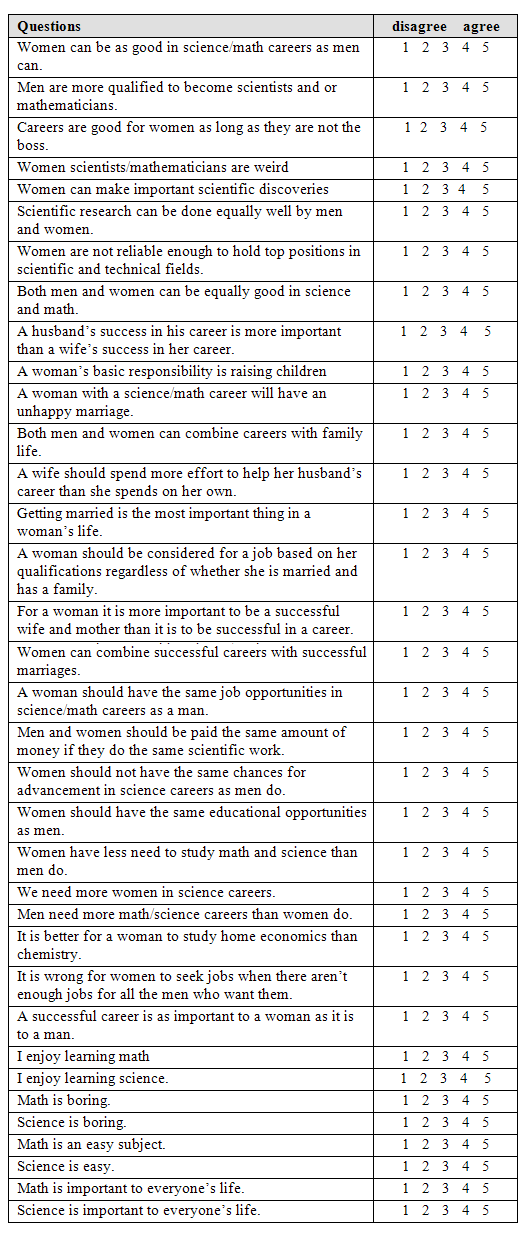
The instrument was a survey questionnaire adapted from the Women in Science Scale (WiSS). The WiSS was chosen for adaptation because it has proven to be a “valuable instrument for basic research or curriculum evaluation where adolescent attitude toward women in science careers is a variable of interest…and [it] could appropriately be used over a wider age range” (Smith & Erb, 1986, p. 668) . Students were asked to complete this questionnaire asking questions about their beliefs, attitudes, confidence, and general comments related to math, science, and technology. There were a total of 48 questions (including 5 questions about demographic information) asked in the survey. The focus of this study is on both mathematics and science, so mathematics was added to explore student attitudes toward this subject. To explore student consideration of a future career, one question asked whether students would consider a math/science-related career (yes/no). See Appendix 1 for the details of the survey.
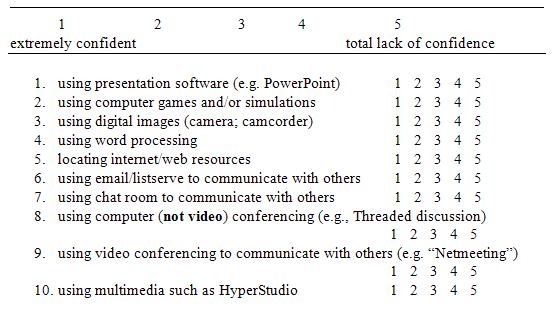
Before analysing data, the items in the questionnaire were first examined qualitatively. Items with similar meanings were grouped together. This similarity was further assessed quantitatively using Cronbach’s alpha which gave the internal consistency of the group. If a group of items possessed high internal consistencies (i.e., with alpha levels higher than .80), these items were collapsed into one variable. For example, the variable “characteristics” were scored on a 5-point Likert scale ranging from 1 (strongly disagree) to 5 (strongly agree) based on 8 items. Sample items included: Women can be as good in science/math careers as men can; Men are more qualified to become scientists and or mathematicians; Careers are good for women as long as they are not the boss. These 8 items were averaged to form the characteristics score. Similarly, 9 items regarding the “compatibility” of women to mathematics and science were scored on a 5-point Likert scale ranging from 1 (strongly disagree) to 5 (strongly agree). Sample items were: A husband’s success in his career is more important than a wife’s success in her career. These 9 items were averaged to form the compatibility score. With respect to the opportunities for women in mathematics and science, 10 items were asked on a 5-point Likert scale ranging from 1 (strongly disagree) to 5 (strongly agree). Items like “Men and women should be paid the same amount of money if they do the same scientific work” were included in this category. These 10 items were averaged to form the “opportunity” score. To gauge students’ attitudes to mathematics and science learning, 8 items were asked on a 5-point Likert scale ranging from 1 (strongly disagree) to 5 (strongly agree). Sample items were: “I enjoy learning math” and “Math is easy.” These 8 items were averaged to form the “attitude” score. Finally, 10 questions regarding confidence with technology were scored on a 5-point Likert scale ranging from 1 (extremely confident) to 5 (total lack of confidence). These 10 questions were averaged to form the “confidence” score. These scores were used in the successive statistical analysis.
Quantitative analysis of the anonymous survey using the Statistical Package for the Social Sciences (SPSS 12.0) was employed to answer the research questions. First, Cronbach’s alpha was calculated for every group of items described above. These alpha values were presented in Table 1.
To explore possible interaction effects of gender and region on student beliefs related to mathematics and science, as well as their confidence of using technology, a two-way MANOVA was conducted. Then the focus was moved to an examination of students’ beliefs about the effectiveness of technology on learning where t-tests were conducted between male and female students as well as between urban and rural students.
The presentation of the results is detailed below, following the order of the research questions asked. The effects of gender and region were examined first, and then the exploration of students’ career considerations in relation to their beliefs.
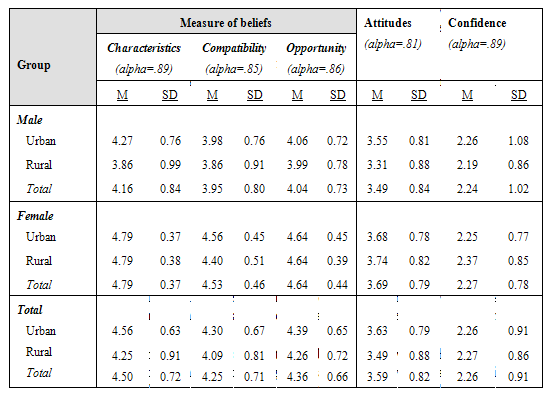
Table 1. Mean and SD by Gender and Region 
Gender and region effects were examined on student beliefs about women in math and science careers, their attitudes toward math and science, and their confidence in using technology. Table 1 presents the means and standard deviations of students’ beliefs, attitudes, and confidence. Particularly, student beliefs were explored through the following three sub-categories: characteristics, compatibility, and opportunity. Table 1 details the descriptive statistics of the five variables.
To examine possible interaction effects, a 2x2 MANOVA was conducted on five dependent variables: characteristics, compatibility, opportunity, attitudes, and confidence. Independent variables were gender (i.e. male vs. female) and region (i.e. urban vs. rural). Table 2 presents the details of the MANOVA results.
Multivariately, there was a significant gender by region interaction effect (F (5,435) =4.94, p<.001), significant gender effect (F (5,435) =0.81, p=.01) and region effect (F (5,435) =0.97, p = .002). Looking at each dependent variable, there was a significant interaction effect (gender by region) on student beliefs about characteristics (F (1, 439) = 7.06, p<.05), but no significant interaction effect on student beliefs about compatibility and opportunity variables, or attitudes and confidence. That is, gender differences in student beliefs about characteristics changed significantly depending on the school region, but there was no significant change for their beliefs about compatibility and opportunity, their attitudes toward math and science, or their confidence in technology use.
Table 2.MANOVA Result of Gender and Region Effect on Beliefs, Attitudes and Confidence 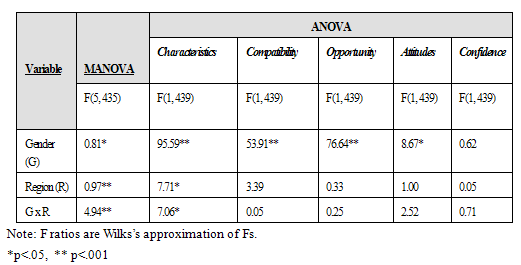
In addition, there were significant gender effects on four dependent variables: characteristics (F (1,439) = 95.59, p<.001), compatibility (F(1,439)= 53.91, p<.001), opportunity (F(1,439)= 76.64, p<.001); and ‘attitudes’ (F(1,439)= 8.67, p<.05). That is, female students, compared to their male peers, were more positive not only about characteristics, compatibility, and opportunity of women in math and science careers, but also in their attitudes toward math and science.
When region was considered, only one significant difference was discerned. The region effect on student beliefs about characteristics was significant (F (1,439) = 7.71, p<.05). That is, urban students held significantly more positive beliefs about characteristics of women in mathematics and science careers than students in rural schools.
The significant gender by region interaction effect on characteristics variable indicated that gender effect varied with region or region effect varies with gender. To further understand the phenomenon, simple effect tests were performed to determine the region effect (gender) on each level of gender (region).
Significant gender effects were identified on both urban and rural student beliefs about characteristics of women in math and science. In urban schools, male students held more positive beliefs about characteristics of women in math and science than female students (F (1, 442) =61.42, p<.001). By contrast, male rural students compared to female rural students held more negative beliefs about the characteristics of women in math and science (F(1, 442)= 48.70, p<.001).
Further, the result showed that there was a significant region effect on male student beliefs about characteristics of women in math and science. Therefore, for females, their beliefs about characteristics of women in math and science did not change depending on urban or rural schools (F (1, 442) =.01, p=.94). Male students in urban schools, however, held more positive beliefs about the characteristics of women in math and science than rural male students (F (1, 442) = 16.33, p<.001).
A t-test was conducted to detect possible gender difference on students’ future career choices. No significant gender difference was found in student consideration of math/science related careers (t (419) =-.017, p=.98).
To examine regional differences in student choice of future career, a t-test was conducted. The significant results (t (425) =-2.3) showed that students in urban schools (mean = 1.22, SD =.42) were more likely to choose science/mathematics related careers than students in rural schools (mean = 1.34, SD =.48).
A t-test was conducted to examine gender difference on student beliefs about the effectiveness of technology. The significant result showed that female students (mean = 1.04, SD = .20), more than male students (mean=1.12, SD = .322), believed that technology was effective for their learning (t (405) =-2.90, p=.004).
Further, a t-test was administrated to test the effect of region on student beliefs about the effectiveness of technology. No significant result was identified (t (408) =-1.18, p=.24).
To examine possible differences on confidence of using technology between students who consider math/science as future career ( i.e., “yes” group) and those who do not (i.e., “no” group), a t-test was conducted. A significant difference was identified between the two groups (t (425) = -2.38, p=.018). “Yes” group (mean = 2.17, SD =.89) were significantly more confident in using technology than the “No” group (mean = 2.41, SD =.93). That is, students who considered math-related and science-related future careers were more confident in using technology than those who did not.
This study sheds light on research related to gender in mathematics, science, and technology. It adds to the literature base in the following ways:
Several conclusions are apparent from the results of this study. First, the significant gender by region effect was found in students’ beliefs about the characteristics of women in math and science. That is, the gender difference in students’ beliefs about women in math and science changes significantly, depending on the location of the school; namely, the difference is smaller in urban schools than in rural schools. Further scrutiny of the data shows that male students in urban schools hold more positive beliefs about women in math and science than male students in rural schools. In urban schools, male students hold more positive beliefs than female students. But in rural schools, male students, compared to their female counterparts, hold more negative beliefs about women in math and science. This suggests that region plays a major role in forming students’ beliefs about mathematics and science. This is significant in that considerable research has demonstrated that children who are quantitatively and scientifically illiterate may be doomed to second-class economic status in modern society (Lee, 2002; Moses, 2001; Schoenfeld, 2002) . The communities in which they reside, such as rural regions, usually suffer economically precisely because the high-technology professions driving the economy will, for the foregoing reason, bypass them (Li & Willing, 2002) . The way to enhance the learning of mathematics, science, and technology for both male and female students, particularly in rural schools, is a critical issue for education.
It was found that, in general, female students in this study have significantly more positive attitudes toward math and science. That is, female students tend to enjoy learning math and science, and think it is more important to learn math and science, than male students do. They also held much more positive beliefs about the characteristics, compatibility, and opportunity of women in math and science careers than male students. This contradicts the TIMSS result that male students tend to hold more positive views about mathematics and science.
Secondly, when the region was considered, significant effects on students’ choice of mathematics- and science-related careers were identified. Urban students, regardless of their gender, were more likely to consider science/mathematics-related careers. One possible reason for this result may relate to role models. Students in urban schools may have more opportunities to observe or find role models such as scientists and mathematicians at universities and research institutions. It is relatively rare to find scientists and mathematicians in rural settings and rural schools are not usually connected to a larger scientific network. The lack of role models, therefore, may affect students’ career decisions.
In particular, it was found that male urban students held much more positive beliefs about the characteristics of women in mathematics and science than male rural students, while females held similar beliefs across regions. This supports the view that rural areas are “schizophrenically conceived of as both the best place to raise children and as a stifling culture of small-town busybodies” (Swanson, 2001, p. 98) . The so-called stifling culture means that certain traditions persist. The tradition that “girls are not good at mathematics and science” may be perpetuated in rural communities.
Thirdly, students who considered mathematics- or science-related careers, compared to those who did not, were more confident in their use of various technologies. This is consistent with the general view that science, mathematics, and technology are interconnected. One implication of this is that the design of technology in schools for mathematics and science should be considered as a package rather than as separate entities.
The results of this study indicate that there is a great deal of work still to be done in education to address the different math, science and technology experiences and views of male and female students in urban and rural schools.
This research was supported by a standard research grant from the Social Sciences and Humanities Research Council (Government of Canada) to the author. The author expresses her appreciation to Dr. Tak Fung for his consultation on statistical analysis, to CJLT editor Dr. Michele Jacobsen and the anonymous reviewers for making valuable suggestions, and to several research assistants for data collection.
Ambrose, R., Levi, L., & Fennema, E. (1997). The complexity of teaching for gender equity. In J. Trentacosta & M. Kennedy (Eds.), Multicultural and gender equity in the mathematics classroom: The gift of diversity. VA: NCTM.
American Association of University Women. (1999). Gender gaps: Where schools still fail our children. Washington, DC: American Association of University Women Educational Foundation.
American Association of University Women. (2000). Tech-savvy: Educating girls in the new computer age. Retrieved August 22, 2002, from http://www.aauw.org/2000/techsavvybd.html
Arnot, M., Gray, J., James, M., Rudduck, J., & Duveen, G. (1998). Recent research on gender and educational performance. London: OFSTED.
Benskin, A. (1994). Black children and underachievement in urban schools. London: Minerva.
Bong, M. (1999). Personal factors effecting the generality of academic self-efficacy judgments: Gender, ethnicity, and relative expertise. The Journal of Experimental Education, 67(4), 315–331.
Carr, M., Jessup, D., & Fuller, D. (1999). Gender differences in first-grade mathematics strategy use: Parent and teacher contributions. Journal for Research in Mathematics Education, 30(1), 20–46.
Connolly, J., Hatchetter, V., & McMaster, L. (1999). Academic achievement in early adolescence: Do school attitudes make a difference. Education Quarterly Review, 6(1), 20–29.
Fennema, E. (2002). Gender equity for mathematics and science. Retrieved August4, 2004, from http://www.woodrow.org/teachers/math/gender/ 02fennema.html
Fennema, E., Carpenter, T., Jacobs, V., Frank, M., & Levi, L. (1998). A longitudinal study of gender differences in young children's mathematical thinking. Educational Rsearcher, 27(5), 6–11.
Fiore, C. (1999). Awakening the tech bug in girls. Learning and Leading with Technology, 26(5), 10–17.
Francis, B. (2000). Boys, girls and achievement: Addressing the classroom issues. London: Taylor & Francis Group.
Hudson, L., & Shafer, L. (2004). Participation in technology-based postcompulsory education. Education Statistics Quarterly, 5(4), 1–7.
Hyde, J. S., Fennema, E., & Lamon, S. J. (1990). Gender differences in mathematics performance: A meta-analysis. Psychological Bulletin, 107, 139–155.
Karp, K. (1998). Feisty females: using children’s literature with strong female characters. Teaching Children Mathematics, 5(2), 8–94.
King, K., & McLeod, D. (1999). Coming of age in academic-A review of mathematics education as a research domain: A search for identity. Journal for Research in Mathematics Education, 30(2), 227–234.
Lee, I. (2002). Gender differences in self-regulated on-line learning strategies within Korea's university context. International Review, 101–111.
Leonard, E. (2003). Women, technology, and the myth of progress. New Jersey: Upper Saddle River: Pearson Education, Inc.
Li, Q., & Willing, L. (2002). Tech_GIRLS: Technology-enhanced gender inclusive role-model learning system. Grant application to National Science Foundation: University of North Dakota.
Lightbody, P., & Durndell, A. (1996). Gendered career choice: Is sex-stereotyping the cause or the consequence? Educational Studies, 22(2), 133–146.
Ma, X. (1999). Dropping out of advanced mathematics: the effects of parental involvement. Teachers College Record, 101(1), 60–81.
McLester, S. (1998). Girls and technology: What’s the story. Technology and Learning, 18–26.
Mid-Atlantic Equity Consortium. (n.d.). Girls: Math and science achievement. Retrieved August, 24, 2004 from http://www.maec.org/
Moses, R. (2001). Radical equations, math literacy and civil rights. Boston: Beacon Press.
Mullis, I., Martin, M., Gonzalez, E., Gregory, K., Garden, R., O'Connor, K., et al. (2000). TIMSS 1999: nternational Mathematics Report. Chestnut Hill, MA: Boston College.
Parker, K. (1999). The impact of the textbook on girls’ perception of mathematics. Mathematics in School, 28(4), 2–4.
Rohrer, J., & Welsh, S. (1998). The Lake Tahoe Watershed project: a summer program for female middle school students in math and science. Roeper Review, 20(4), 288–290.
Sadker, D. (1999). Gender equity: Still knocking at the classroom door. Educational Leadership, 56(7), 22–26.
Sanders, J., & Peterson, K. (1999). Close the gap for girls in math-related careers. The Education Digest, 65(4), 47–49.
Schoenfeld, A. (2002). Making mathematics work for all children: Issues of standards, testing and equity. Educational Researcher, 31(1), 13–25.
Smith, B., & Erb. (1986). Effect of women science career role models on early adolescents' attitudes toward scientists and women in science. Journal of Research in Science Teaching, 23(8), 667–676.
Swanson, L. (2001). Rural opportunities: Minimalist policy and community-based experimentation. Policy Study Journal, 29 , 96–107.
Section one: About You
Section two:
Please answer all the questions. Circle the number which most closely reflects your attitude toward each statement.
1. Would you consider a science/math related career? Yes No
Section three: Your confidence with technology
Please indicate your degree of confidence in using the technology as described based on the following:
Section four: Your belief about use of technology
Please comment in writing on the use of technology in your learning:
© Canadian Journal of Learning and Technology